How To Find Slope With Y Mx B

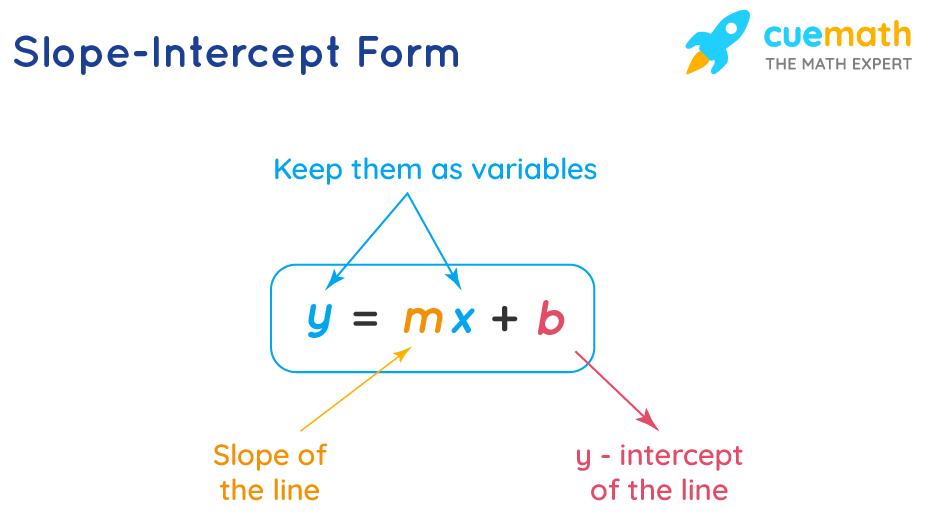
y=mx+b

y = mx + b is the slope intercept class of writing the equation of a straight line. In the equation 'y = mx + b', 'b' is the signal, where the line intersects the 'y axis' and 'thousand' denotes the slope of the line. The gradient or gradient of a line describes how steep a line is. It can have either a positive or a negative value. When a standard form of a linear equation is of the class Ax + By  = C, where 'x' and 'y'  and 'C' are variables and 'A', 'B' are constants, the slope-intercept form is the most preferred way of expressing a direct line due to its simplicity, as information technology is very easy to find the slope and the 'y intercept' from the given equation.

1.	Meaning of y = mx + b
2.	How to Find y = mx + b?
3.	Writing an Equation in the Slope Intercept Form
four.	Solved Examples on y mx b
5.	Practice Questions on y mx b
6.	FAQs on y mx b

Meaning of y = mx + b

y = mx + b is the slope-intercept form of a staight line. In the equation y = mx + b for a directly line, m is called the slope of the line and b is the y-intercept of a line. y = mx+b, where

y ⇒  how far upwards or downwardly is the line,

x  ⇒ how far along is the line,

b ⇒ the value of y when ten = 0 and

thousand ⇒ how steep the line is.

This is determined past m = (difference in y coordinates)/ (difference in x coordinates). Annotation that difference in y coordinates is indicated as rise or fall and difference in x coordinates is indicated equally run.

How To Find y = mx + b?

y = mx + b is the formula used to find the equation of a straight line, when we know the gradient(chiliad) and the y-intercept (b) of the line. To determine k, we apply a formula based on the calculations. Permit's derive this formula using the equation for the slope of a line. Let us consider a line whose gradient is 'm' and whose y-intercept is 'b'. Let (x,y) be any other random bespeak on the line whose coordinates are not known. We obtain the graph equally follows.

We know that the equation for the slope of a line in the slope-intercept form is y = mx+b

Rewriting this, we get one thousand = (y-b) / x

Thus the formula to find k = change in y/ change in ten

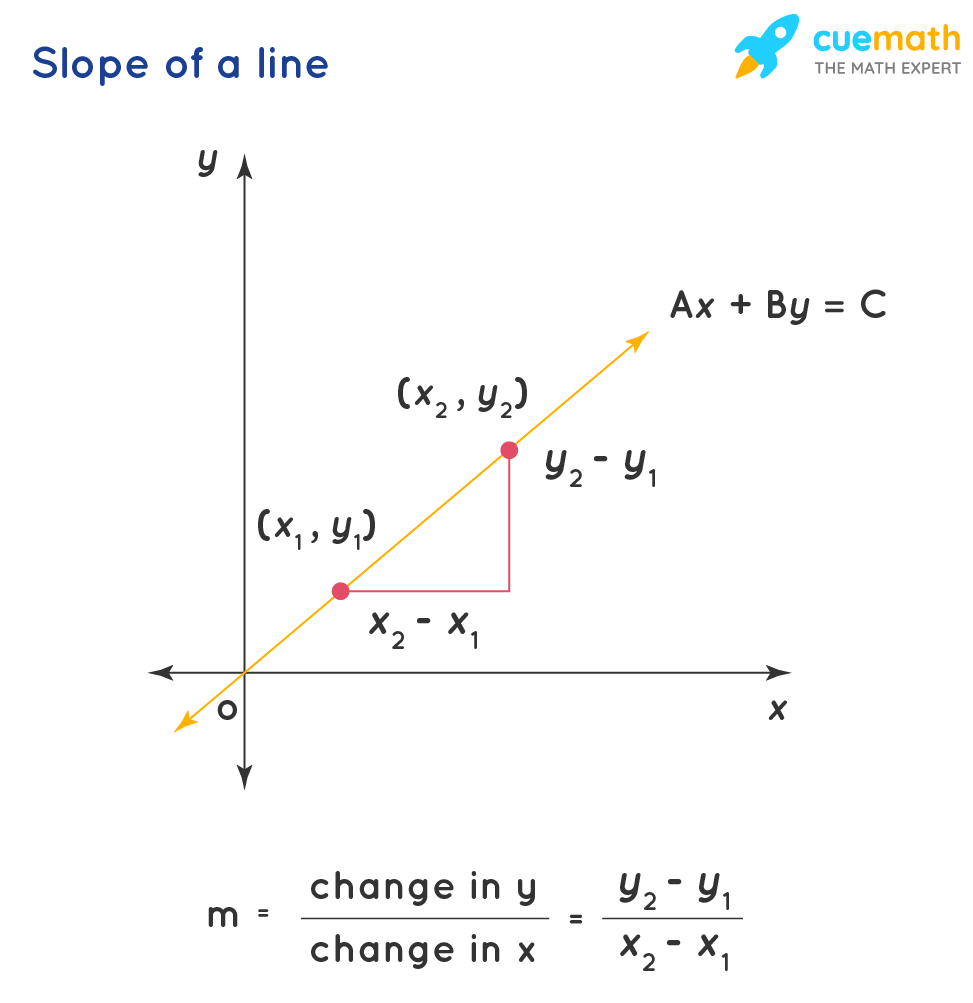
Permit us derive the formula to find the value of the slope if two points \((x_{i},y_{i})\) and \((x_{2},y_{two})\) on the straight line are known. And so we take \(y_{1} = mx_{1} + b\) and \(y_{ii} = mx_{2} + b\)

We know that, gradient = change in y/ change in x

Substituting the values of y₁ and y_ii, we become \[\begin{marshal}\dfrac{y_{2}-y_{ane}}{x_{2}-x_{i}}&= \dfrac{(mx_{2}+b) - (mx_{i}+b)}{x_{2}-x_{i}}\\\\&=\dfrac{mx_{2}-mx_{1}}{x_{2}-x_{one}}\\\\&= \dfrac{m(x_{2}-x_{one})}{x_{ii}-x_{one}}\\\\ &=m\end{marshal}\]

Thus we find that the gradient (m) is calculated equally (alter in y)/ (modify in x)

m = (difference in y coordinates)/ (departure in x coordinates)

To find the y-intercept or 'b', substitute the value of '10' every bit 0 in the equation of a straight line, which is of the grade Ax + Past + C = 0. Consider an equation of a direct line : 3x + 5y = 10. To discover the y-intercept, substitute the value of '10' every bit 0 in the equation and solve for 'y'. On substituting 'x = 0' in the equation 3x + 5y =10, nosotros get, 3(0) + 5y = 10
⇒5y = 10 and thus y = ten/5 ⇒ y = 2 or 'b' = 2.

Writing an Equation in The Slope Intercept Course

If the gradient 'm' and y-intercept 'b' are given, and so the equation of the directly line tin can be written in the class of 'y = mx +b'. For case, if the slope(m) for a line is two and the y-intercept 'b' is -1, and so the equation of the straight line is written as y = 2x - i.  The gradient value can be positive or negative. Equally we discussed in the earlier sections, in y = mx + b, 'thou' represents the slope of the equation. To find the slope of a line, given its equation, we have to rearrange its terms to the gradient-intercept class y = mx + b. Here, 'm' gives the slope and 'b'  gives the y-intercept of the equation.

Permit usa consider the equation 2x + 3y = six. We are required to find the slope and the y-intercept from the equation which is of the form Ax + Past = C

We rewrite the standard grade of the equation of the line to the slope-intercept grade y = mx + b.

2x + 3y = half-dozen
3y = 2x + vi
y = (-2/iii) x + 2

Comparing the final equation with y = mx + b, nosotros obtain the slope of the equation is m = -2/iii and the y-intercept of the equation is, b = 2 or (0,two).

Important Notes:

• The equation of the gradient-intercept form of a line whose slope is 'm' and whose y-intercept is 'b' or (0,b) is y = mx + b.
• The equation of a horizontal line passing through (a,b) is of the form y = b.
• The equation of a vertical line passing through (a,b) is of the form x = a.
• m is calculated using the formula rising over run or (change in y)/ (change in 10)

Topics Related to y = mx + b

Cheque out some interesting articles related to y = mx + b.

• Linear Equation Formula
• Equation of a Directly Line
• Linear Equations
• Linear Equations and Half Planes
• Point-slope formula
• Two Point Form

1. Example 1: Discover the equation of the line whose graph contains the points (ane,3) and (three,vii)

   Solution:
   The required equation of the line is y = mx + b
   Using the formula for slope, m = change in y / change in x = \(\dfrac{y_{2}-y_{i}}{x_{two}-x_{1}}\)
   = (7-iii)/ (three-1) = iv/2 ⇒ thousand = two
   To discover the y-intercept b, we consider any one of the coordinates.
   Let the states use(1,three) and 1000 = 2 and substitute the values in the equation \(y_{one} = mx_{one} + b\)
   three = 2(1) + b ⇒ b = 3 - 2 = 1
   Applying, m =ii and b = 1 in the equation of the line(y = mx + b), nosotros get y = 2x + 1 Thus the equation of the straight line is y = 2x + 1

2. Example 2: Find the slope-intercept form of a line with slope -2 and which passes through the point (-1.4).

   Solution:
   We know that the gradient-intercept course of a line is y = mx + b.
   It is given that slope (thousand) = -2 and the coordinates through which the line is passing through is (-1,4).  Substituting the given values in the slope-intercept class equation we get,  4 = (-2) (-1) + b.
   4 = 2 + b b = 4 - ii = 2.
   The slope intercept form of the line is  y = - two x + ii.

become to slidego to slide

Have questions on basic mathematical concepts?

Get a problem-solving champ using logic, non rules. Larn the why behind math with our certified experts

Book a Free Trial Class

FAQs on y mx b

What is y = mx + b?

y = mx + b is a representation of equation of a directly line. Information technology is called every bit the gradient intercept form. 'm' is referred to as the slope of the line, and 'b' refers to the 'y -intercept' of the line.

How to Detect the Slope of a Line?

For two coordinates, (x₁,y_i) and (ten₂, y₂), the slope of a line is the ratio of difference between the deviation between the y coordinates and the deviation between 10 coordinates, besides known every bit the ascension over the run. The formula to detect the slope of a line is m = (y₂-y_i)/(x₂-x₁)

What is Slope-Intercept Form?

The equation of a directly line which is of the form y = mx + b, is called the gradient intercept form. Here 'm' is the slope of the line and 'b' is the point at which the line intercepts the y - centrality. An example for slope intercept form equation is y = 3x + 5

What is a Line With a Negative Slope?

A line for which the slope in negative is said to movement from left to right in a graph. The slope of a line is constitute by the ration of deviation in y-coordinates to the divergence in x-coordinates. If this value is negative for a line, and so the line has a negative slope.

What Does the Gradient of a Line Mean?

The direction of a line is described by its slope. The gradient tin can be positive or negative, based on its management. A negative gradient moves down from left to right and a line with positive gradient moves in the upward direction from right to left.

Source: https://www.cuemath.com/geometry/y-mx-b/

Posted by: cobbposis1961.blogspot.com

Share this post