How To Find Area Of Arc Length

Altitude along a curve

When rectified, the curve gives a straight line segment with the same length equally the curve's arc length.

Arc length is the distance between two points forth a section of a curve.

Determining the length of an irregular arc segment is too chosen rectification of a curve. The advent of infinitesimal calculus led to a general formula that provides closed-form solutions in some cases.

General arroyo [edit]

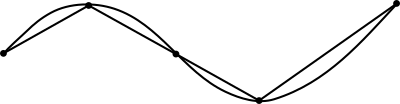
Approximation by multiple linear segments

A curve in the airplane can be approximated by connecting a finite number of points on the curve using line segments to create a polygonal path. Since information technology is straightforward to summate the length of each linear segment (using the Pythagorean theorem in Euclidean infinite, for example), the total length of the approximation can be found past summation of the lengths of each linear segment; that approximation is known as the (cumulative) chordal distance.^[one]

If the curve is non already a polygonal path, using a progressively larger number of segments of smaller lengths volition consequence in better approximations. The lengths of the successive approximations volition non subtract and may keep increasing indefinitely, only for smooth curves they will tend to a finite limit as the lengths of the segments get arbitrarily minor.

For some curves there is a smallest number ${\displaystyle L}$ that is an upper bound on the length of all polygonal approximations. These curves are called rectifiable and the arc length is defined as the number ${\displaystyle L}$ .

Formula for a smooth curve [edit]

Let ${\displaystyle f\colon [a,b]\to \mathbb {R} ^{due north}}$ be an injective and continuously differentiable function. The length of the curve defined by ${\displaystyle f}$ can be divers as the limit of the sum of line segment lengths for a regular division of ${\displaystyle [a,b]}$ as the number of segments approaches infinity. This means

$${\displaystyle L(f)=\lim _{Northward\to \infty }\sum _{i=ane}^{N}{\bigg |}f(t_{i})-f(t_{i-1}){\bigg |}}$$

where ${\displaystyle t_{i}=a+i(b-a)/Northward=a+i\Delta t}$ for ${\displaystyle i=0,1,\dotsc ,North.}$ This definition is equivalent to the standard definition of arc length as an integral:

$${\displaystyle \lim _{N\to \infty }\sum _{i=1}^{Northward}{\bigg |}f(t_{i})-f(t_{i-i}){\bigg |}=\lim _{N\to \infty }\sum _{i=i}^{Due north}\left|{\frac {f(t_{i})-f(t_{i-1})}{\Delta t}}\right|\Delta t=\int _{a}^{b}{\Large |}f'(t){\Large |}\ dt.}$$

The last equality above is truthful because of the following: (i) by the fundamental theorem of calculus, ${\displaystyle f(t_{i})-f(t_{i-1})=\Delta t\int _{0}^{1}f'(\theta t_{i}+(one-\theta )t_{i-1})\ d\theta }$ ; (2) the function ${\displaystyle \left|f'\correct|}$ is continuous, thus it is uniformly continuous, so in that location is a positive real function ${\displaystyle \delta (\varepsilon )}$ of positive real ${\displaystyle \varepsilon }$ such that ${\displaystyle \Delta t<\delta (\varepsilon )}$ implies ${\displaystyle \left|\left|f'(t_{i-1}+\theta _{i}(t_{i}-t_{i-ane}))\correct|-\left|f'(t_{i})\right|\right|<\varepsilon .}$ This ways

$${\displaystyle \sum _{i=1}^{Northward}\left|{\frac {f(t_{i})-f(t_{i-1})}{\Delta t}}\correct|\Delta t-\sum _{i=one}^{N}{\Big |}f'(t_{i}){\Big |}\Delta t}$$

has accented value less than ${\displaystyle \varepsilon (b-a)}$ for ${\displaystyle N>(b-a)/\delta (\varepsilon ).}$ This means that in the limit ${\displaystyle N\to \infty ,}$ the left term higher up equals the right term, which is but the Riemann integral of ${\displaystyle \left|f'(t)\right|}$ on ${\displaystyle [a,b].}$ This definition of arc length shows that the length of a bend ${\displaystyle f:[a,b]\to \mathbb {R} ^{due north}}$ continuously differentiable on ${\displaystyle [a,b]}$ is ever finite. In other words, the curve is always rectifiable.

The definition of arc length of a smooth curve as the integral of the norm of the derivative is equivalent to the definition

$${\displaystyle L(f)=\sup \sum _{i=1}^{North}{\bigg |}f(t_{i})-f(t_{i-1}){\bigg |}}$$

where the supremum is taken over all possible partitions ${\displaystyle a=t_{0}<t_{1}<\dots <t_{N-1}<t_{N}=b}$ of ${\displaystyle [a,b].}$ ^[ii] This definition is also valid if ${\displaystyle f}$ is merely continuous, non differentiable.

A curve tin can be parameterized in infinitely many ways. Let ${\displaystyle \varphi :[a,b]\to [c,d]}$ be any continuously differentiable bijection. And then ${\displaystyle grand=f\circ \varphi ^{-i}:[c,d]\to \mathbb {R} ^{n}}$ is another continuously differentiable parameterization of the curve originally divers past ${\displaystyle f.}$ The arc length of the curve is the same regardless of the parameterization used to define the curve:

$${\displaystyle {\brainstorm{aligned}L(f)&=\int _{a}^{b}{\Big |}f'(t){\Big |}\ dt=\int _{a}^{b}{\Big |}g'(\varphi (t))\varphi '(t){\Big |}\ dt\\&=\int _{a}^{b}{\Large |}g'(\varphi (t)){\Large |}\varphi '(t)\ dt\quad {\text{in the case of }}\varphi {\text{ being non-decreasing}}\\&=\int _{c}^{d}{\Big |}g'(u){\Big |}\ du\quad {\text{using integration by substitution}}\\&=Fifty(m).\end{aligned}}}$$

Finding arc lengths by integrating [edit]

If a planar curve in ${\displaystyle \mathbb {R} ^{2}}$ is defined past the equation ${\displaystyle y=f(x),}$ where ${\displaystyle f}$ is continuously differentiable, then it is just a special example of a parametric equation where ${\displaystyle x=t}$ and ${\displaystyle y=f(t).}$ The Euclidean distance of each infinitesimal segment of the arc tin can be given by:

$${\displaystyle {\sqrt {dx^{2}+dy^{2}}}={\sqrt {i+\left({\frac {dy}{dx}}\correct)^{ii}\,}}dx.}$$

The arc length is then given by:

$${\displaystyle s=\int _{a}^{b}{\sqrt {one+\left({\frac {dy}{dx}}\right)^{ii}\,}}dx.}$$

Curves with closed-course solutions for arc length include the catenary, circumvolve, cycloid, logarithmic screw, parabola, semicubical parabola and straight line. The lack of a airtight grade solution for the arc length of an elliptic and hyperbolic arc led to the development of the elliptic integrals.

Numerical integration [edit]

In nearly cases, including even simple curves, there are no closed-form solutions for arc length and numerical integration is necessary. Numerical integration of the arc length integral is usually very efficient. For example, consider the problem of finding the length of a quarter of the unit circumvolve by numerically integrating the arc length integral. The upper one-half of the unit circle can be parameterized as ${\displaystyle y={\sqrt {1-ten^{ii}}}.}$ The interval ${\displaystyle x\in \left[-{\sqrt {2}}/2,{\sqrt {2}}/2\right]}$ corresponds to a quarter of the circle. Since ${\textstyle dy/dx=-ten/{\sqrt {1-x^{2}}}}$ and ${\displaystyle 1+(dy/dx)^{two}=1/\left(1-x^{ii}\right),}$ the length of a quarter of the unit circle is

$${\displaystyle \int _{-{\sqrt {2}}/2}^{{\sqrt {two}}/2}{\frac {dx}{\sqrt {one-10^{2}}}}\,.}$$

The 15-betoken Gauss–Kronrod rule estimate for this integral of ane.570796 326 808 177 differs from the true length of

$${\displaystyle {\Big [}\arcsin ten{\Big ]}_{-{\sqrt {2}}/2}^{{\sqrt {2}}/2}={\frac {\pi }{2}}}$$

by i.three×ten⁻¹¹ and the 16-signal Gaussian quadrature rule judge of 1.570796 326 794 727 differs from the true length by just 1.7×10^−thirteen . This ways it is possible to evaluate this integral to near machine precision with only 16 integrand evaluations.

Curve on a surface [edit]

Allow ${\displaystyle \mathbf {x} (u,v)}$ exist a surface mapping and permit ${\displaystyle \mathbf {C} (t)=(u(t),v(t))}$ be a curve on this surface. The integrand of the arc length integral is ${\displaystyle \left|\left(\mathbf {10} \circ \mathbf {C} \right)'(t)\correct|.}$ Evaluating the derivative requires the chain dominion for vector fields:

$${\displaystyle D(\mathbf {x} \circ \mathbf {C} )=(\mathbf {x} _{u}\ \mathbf {10} _{v}){\binom {u'}{v'}}=\mathbf {ten} _{u}u'+\mathbf {x} _{v}five'.}$$

The squared norm of this vector is

$${\displaystyle \left(\mathbf {10} _{u}u'+\mathbf {x} _{five}5'\right)\cdot (\mathbf {ten} _{u}u'+\mathbf {10} _{5}v')=g_{eleven}\left(u'\right)^{2}+2g_{12}u'five'+g_{22}\left(v'\right)^{2}}$$

(where ${\displaystyle g_{ij}}$ is the kickoff fundamental grade coefficient), so the integrand of the arc length integral can be written as ${\displaystyle {\sqrt {g_{ab}\left(u^{a}\right)'\left(u^{b}\right)'\,}}}$ (where ${\displaystyle u^{one}=u}$ and ${\displaystyle u^{2}=v}$ ).

Other coordinate systems [edit]

Let ${\displaystyle \mathbf {C} (t)=(r(t),\theta (t))}$ exist a curve expressed in polar coordinates. The mapping that transforms from polar coordinates to rectangular coordinates is

$${\displaystyle \mathbf {x} (r,\theta )=(r\cos \theta ,r\sin \theta ).}$$

The integrand of the arc length integral is ${\displaystyle \left|\left(\mathbf {x} \circ \mathbf {C} \right)'(t)\right|.}$ The chain dominion for vector fields shows that ${\displaystyle D(\mathbf {x} \circ \mathbf {C} )=\mathbf {ten} _{r}r'+\mathbf {10} _{\theta }\theta '.}$ So the squared integrand of the arc length integral is

$${\displaystyle \left(\mathbf {x_{r}} \cdot \mathbf {x_{r}} \right)\left(r'\right)^{two}+2\left(\mathbf {x} _{r}\cdot \mathbf {x} _{\theta }\right)r'\theta '+\left(\mathbf {x} _{\theta }\cdot \mathbf {x} _{\theta }\right)\left(\theta '\right)^{2}=\left(r'\correct)^{2}+r^{two}\left(\theta '\right)^{2}.}$$

So for a curve expressed in polar coordinates, the arc length is

$${\displaystyle \int _{t_{1}}^{t_{ii}}{\sqrt {\left({\frac {dr}{dt}}\right)^{2}+r^{2}\left({\frac {d\theta }{dt}}\right)^{2}\,}}dt=\int _{\theta (t_{i})}^{\theta (t_{2})}{\sqrt {\left({\frac {dr}{d\theta }}\right)^{2}+r^{two}\,}}d\theta .}$$

Now allow ${\displaystyle \mathbf {C} (t)=(r(t),\theta (t),\phi (t))}$ be a curve expressed in spherical coordinates where ${\displaystyle \theta }$ is the polar angle measured from the positive ${\displaystyle z}$ -axis and ${\displaystyle \phi }$ is the azimuthal angle. The mapping that transforms from spherical coordinates to rectangular coordinates is

$${\displaystyle \mathbf {x} (r,\theta ,\phi )=(r\sin \theta \cos \phi ,r\sin \theta \sin \phi ,r\cos \theta ).}$$

Using the chain rule once more shows that ${\displaystyle D(\mathbf {10} \circ \mathbf {C} )=\mathbf {x} _{r}r'+\mathbf {x} _{\theta }\theta '+\mathbf {10} _{\phi }\phi '.}$ All dot products ${\displaystyle \mathbf {x} _{i}\cdot \mathbf {x} _{j}}$ where ${\displaystyle i}$ and ${\displaystyle j}$ differ are zippo, so the squared norm of this vector is

$${\displaystyle \left(\mathbf {x} _{r}\cdot \mathbf {x} _{r}\right)\left(r'^{ii}\right)+\left(\mathbf {x} _{\theta }\cdot \mathbf {x} _{\theta }\correct)\left(\theta '\right)^{2}+\left(\mathbf {x} _{\phi }\cdot \mathbf {x} _{\phi }\right)\left(\phi '\right)^{two}=\left(r'\right)^{2}+r^{two}\left(\theta '\right)^{2}+r^{two}\sin ^{2}\theta \left(\phi '\right)^{two}.}$$

And then for a bend expressed in spherical coordinates, the arc length is

$${\displaystyle \int _{t_{1}}^{t_{2}}{\sqrt {\left({\frac {dr}{dt}}\right)^{two}+r^{two}\left({\frac {d\theta }{dt}}\right)^{ii}+r^{2}\sin ^{2}\theta \left({\frac {d\phi }{dt}}\right)^{ii}\,}}dt.}$$

A very like calculation shows that the arc length of a bend expressed in cylindrical coordinates is

$${\displaystyle \int _{t_{1}}^{t_{2}}{\sqrt {\left({\frac {dr}{dt}}\right)^{2}+r^{two}\left({\frac {d\theta }{dt}}\right)^{2}+\left({\frac {dz}{dt}}\right)^{2}\,}}dt.}$$

Uncomplicated cases [edit]

Arcs of circles [edit]

Arc lengths are denoted by s, since the Latin give-and-take for length (or size) is spatium.

In the post-obit lines, ${\displaystyle r}$ represents the radius of a circle, ${\displaystyle d}$ is its diameter, ${\displaystyle C}$ is its circumference, ${\displaystyle s}$ is the length of an arc of the circle, and ${\displaystyle \theta }$ is the bending which the arc subtends at the centre of the circle. The distances ${\displaystyle r,d,C,}$ and ${\displaystyle southward}$ are expressed in the same units.

• ${\displaystyle C=two\pi r,}$ which is the same every bit ${\displaystyle C=\pi d.}$ This equation is a definition of ${\displaystyle \pi .}$
• If the arc is a semicircle, and then ${\displaystyle south=\pi r.}$
• For an arbitrary circular arc:
  • If ${\displaystyle \theta }$ is in radians then ${\displaystyle due south=r\theta .}$ This is a definition of the radian.
  • If ${\displaystyle \theta }$ is in degrees, then ${\displaystyle due south={\frac {\pi r\theta }{180^{\circ }}},}$ which is the same as ${\displaystyle s={\frac {C\theta }{360^{\circ }}}.}$
  • If ${\displaystyle \theta }$ is in grads (100 grads, or grades, or gradians are i right-bending), then ${\displaystyle southward={\frac {\pi r\theta }{200{\text{ grad}}}},}$ which is the same equally ${\displaystyle due south={\frac {C\theta }{400{\text{ grad}}}}.}$
  • If ${\displaystyle \theta }$ is in turns (1 plough is a complete rotation, or 360°, or 400 grads, or ${\displaystyle 2\pi }$ radians), and then ${\displaystyle s=C\theta /one{\text{ turn}}}$ .

Great circles on Earth [edit]

Two units of length, the nautical mile and the metre (or kilometre), were originally divers and so the lengths of arcs of great circles on the Earth's surface would be merely numerically related to the angles they subtend at its centre. The simple equation ${\displaystyle southward=\theta }$ applies in the following circumstances:

The lengths of the distance units were chosen to brand the circumference of the World equal 40000 kilometres, or 21600 nautical miles. Those are the numbers of the respective angle units in one complete turn.

Those definitions of the metre and the nautical mile have been superseded past more precise ones, merely the original definitions are still authentic enough for conceptual purposes and some calculations. For example, they imply that one kilometre is exactly 0.54 nautical miles. Using official modern definitions, 1 nautical mile is exactly ane.852 kilometres,^[three] which implies that 1 kilometre is nigh 0.539956 80 nautical miles.^[4] This modern ratio differs from the 1 calculated from the original definitions by less than one function in ten,000.

Other simple cases [edit]

• Archimedean spiral § Arc length
• Cycloid § Arc length
• Ellipse § Arc length
• Helix § Arc length
• Parabola § Arc length
• Sine and cosine § Arc length
• Triangle moving ridge § Arc length

Historical methods [edit]

Artifact [edit]

For much of the history of mathematics, even the greatest thinkers considered it impossible to compute the length of an irregular arc. Although Archimedes had pioneered a manner of finding the area beneath a bend with his "method of exhaustion", few believed it was even possible for curves to have definite lengths, as practice straight lines. The first ground was cleaved in this field, as it often has been in calculus, by approximation. People began to inscribe polygons inside the curves and compute the length of the sides for a somewhat accurate measurement of the length. By using more segments, and by decreasing the length of each segment, they were able to obtain a more than and more accurate approximation. In detail, by inscribing a polygon of many sides in a circle, they were able to find approximate values of π.^{[five] [6]}

17th century [edit]

In the 17th century, the method of burnout led to the rectification by geometrical methods of several transcendental curves: the logarithmic screw by Evangelista Torricelli in 1645 (some sources say John Wallis in the 1650s), the cycloid by Christopher Wren in 1658, and the ambit by Gottfried Leibniz in 1691.

In 1659, Wallis credited William Neile'south discovery of the outset rectification of a nontrivial algebraic curve, the semicubical parabola.^[7] The accompanying figures appear on folio 145. On folio 91, William Neile is mentioned every bit Gulielmus Nelius.

Integral form [edit]

Before the full formal evolution of calculus, the basis for the modern integral class for arc length was independently discovered by Hendrik van Heuraet and Pierre de Fermat.

In 1659 van Heuraet published a construction showing that the problem of determining arc length could be transformed into the trouble of determining the surface area under a curve (i.eastward., an integral). As an instance of his method, he determined the arc length of a semicubical parabola, which required finding the area under a parabola.^[8] In 1660, Fermat published a more general theory containing the aforementioned outcome in his De linearum curvarum cum lineis rectis comparatione dissertatio geometrica (Geometric dissertation on curved lines in comparison with straight lines).^[nine]

Fermat's method of determining arc length

Building on his previous work with tangents, Fermat used the bend

${\displaystyle y=x^{\frac {3}{ii}}\,}$

whose tangent at ten = a had a slope of

${\displaystyle {3 \over 2}a^{\frac {one}{2}}}$

so the tangent line would take the equation

${\displaystyle y={three \over 2}a^{\frac {i}{2}}(x-a)+f(a).}$

Next, he increased a by a pocket-size amount to a + ε, making segment Air-conditioning a relatively good approximation for the length of the bend from A to D. To find the length of the segment Air conditioning, he used the Pythagorean theorem:

${\displaystyle {\begin{aligned}Air-conditioning^{two}&=AB^{two}+BC^{2}\\&=\varepsilon ^{2}+{ix \over 4}a\varepsilon ^{two}\\&=\varepsilon ^{2}\left(1+{nine \over iv}a\right)\stop{aligned}}}$

which, when solved, yields

${\displaystyle Air conditioning=\varepsilon {\sqrt {1+{nine \over iv}a\,}}.}$

In order to estimate the length, Fermat would sum up a sequence of short segments.

Curves with infinite length [edit]

As mentioned above, some curves are non-rectifiable. That is, there is no upper bound on the lengths of polygonal approximations; the length tin exist made arbitrarily big. Informally, such curves are said to have infinite length. There are continuous curves on which every arc (other than a single-signal arc) has space length. An instance of such a bend is the Koch curve. Another example of a curve with infinite length is the graph of the function defined past f(x) =x sin(1/x) for whatsoever open set with 0 every bit i of its delimiters and f(0) = 0. Sometimes the Hausdorff dimension and Hausdorff measure out are used to quantify the size of such curves.

Generalization to (pseudo-)Riemannian manifolds [edit]

Let ${\displaystyle M}$ exist a (pseudo-)Riemannian manifold, ${\displaystyle \gamma :[0,1]\rightarrow M}$ a curve in ${\displaystyle One thousand}$ and ${\displaystyle thou}$ the (pseudo-) metric tensor.

The length of ${\displaystyle \gamma }$ is defined to be

$${\displaystyle \ell (\gamma )=\int _{0}^{ane}{\sqrt {\pm g\left(\gamma '(t),\gamma '(t)\right)\,}}dt,}$$

where ${\displaystyle \gamma '(t)\in T_{\gamma (t)}Grand}$ is the tangent vector of ${\displaystyle \gamma }$ at ${\displaystyle t.}$ The sign in the square root is chosen one time for a given bend, to ensure that the foursquare root is a real number. The positive sign is chosen for spacelike curves; in a pseudo-Riemannian manifold, the negative sign may be called for timelike curves. Thus the length of a curve is a non-negative real number. Unremarkably no curves are considered which are partly spacelike and partly timelike.

In theory of relativity, arc length of timelike curves (world lines) is the proper time elapsed forth the globe line, and arc length of a spacelike curve the proper distance forth the curve.

Meet also [edit]

• Arc (geometry)
• Circumference
• Crofton formula
• Elliptic integral
• Geodesics
• Intrinsic equation
• Integral approximations
• Line integral
• Superlative arc
• Multivariable calculus
• Sinuosity

References [edit]

1. ^ Ahlberg; Nilson (1967). The Theory of Splines and Their Applications . Bookish Press. p. 51. ISBN9780080955452.
2. ^ Rudin, Walter (1976). Principles of Mathematical Assay . McGraw-Hill, Inc. pp. 137. ISBN978-0-07-054235-eight.
3. ^ Suplee, Curt (2 July 2009). "Special Publication 811". nist.gov.
4. ^ CRC Handbook of Chemistry and Physics, p. F-254
5. ^ Richeson, David (May 2015). "Round Reasoning: Who Kickoff Proved That C Divided past d Is a Constant?". The Higher Mathematics Journal. 46 (3): 162–171. doi:x.4169/higher.math.j.46.3.162. ISSN 0746-8342. S2CID 123757069.
6. ^ Coolidge, J. L. (February 1953). "The Lengths of Curves". The American Mathematical Monthly. 60 (2): 89–93. doi:10.2307/2308256. JSTOR 2308256.
7. ^ Wallis, John (1659). Tractatus Duo. Prior, De Cycloide et de Corporibus inde Genitis…. Oxford: University Press. pp. 91–96.
8. ^ van Heuraet, Hendrik (1659). "Epistola de transmutatione curvarum linearum in rectas [Letter on the transformation of curved lines into right ones]". Renati Des-Cartes Geometria (2nd ed.). Amsterdam: Louis & Daniel Elzevir. pp. 517–520.
9. ^ M.P.E.A.Southward. (pseudonym of Fermat) (1660). De Linearum Curvarum cum Lineis Rectis Comparatione Dissertatio Geometrica. Toulouse: Arnaud Colomer.

Sources [edit]

• Farouki, Rida T. (1999). "Curves from motion, motion from curves". In Laurent, P.-J.; Sablonniere, P.; Schumaker, 50. L. (eds.). Curve and Surface Design: Saint-Malo 1999. Vanderbilt Univ. Press. pp. 63–90. ISBN978-0-8265-1356-4.

External links [edit]

Wikimedia Commons has media related to Arc length.

• "Rectifiable curve", Encyclopedia of Mathematics, European monetary system Press, 2001 [1994]
• The History of Curvature
• Weisstein, Eric W. "Arc Length". MathWorld.
• Arc Length past Ed Pegg Jr., The Wolfram Demonstrations Project, 2007.
• Calculus Study Guide – Arc Length (Rectification)
• Famous Curves Index The MacTutor History of Mathematics annal
• Arc Length Approximation by Republic of chad Pierson, Josh Fritz, and Angela Sharp, The Wolfram Demonstrations Project.
• Length of a Bend Experiment Illustrates numerical solution of finding length of a curve.

Source: https://en.wikipedia.org/wiki/Arc_length

Posted by: cobbposis1961.blogspot.com

Share this post